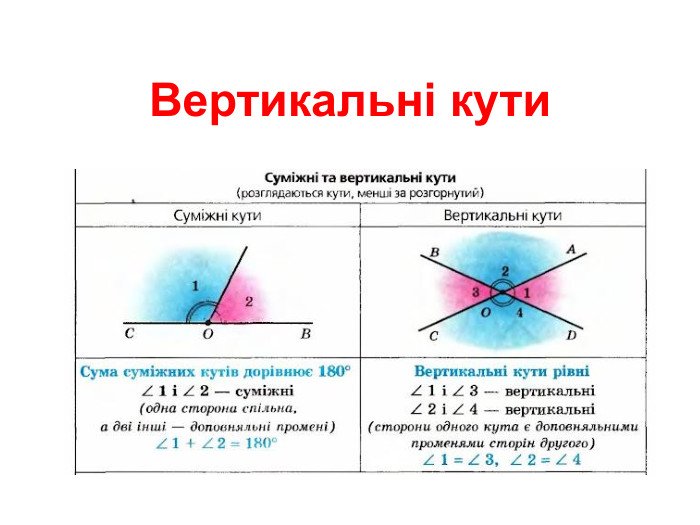
Що таке вертикальні кути
Що таке вертикальні кути? Це одне з ключових понять у геометрії, яке допомагає зрозуміти не лише абстрактні математичні концепції, але і безліч практичних аспектів в архітектурі, інженерії, і навіть у повсякденному житті.
Вступ до поняття вертикальних кутів
Вертикальні кути — це пари кутів, що утворюються при перетині двох прямих. Ключова їхня характеристика — рівність між собою. Це означає, що якщо ми маємо перетин двох ліній, то кути, які не сусідні при цьому перетині, завжди дорівнюють один одному. І саме це дозволяє нам застосовувати знання про вертикальні кути у численних задачах математичного та практичного характеру.
Ідентифікація вертикальних кутів
Для аналізу вертикальних кутів нам варто спочатку розглянути процес їх утворення і властивості:
- Коли дві прямі перетинаються, утворюються дві пари вертикальних кутів.
- Вертикальні кути характеризуются тим, що вони рівні один одному.
- Отже, якщо відомий вимір одного з них, інший автоматично має таке ж значення.
Характеристики вертикальних кутів
Однією з ключових особливостей вертикальних кутів є їх рівність. Це дозволяє використовувати їх у різних розрахунках і твердженнях, які обираються в геометрії. Давайте детальніше розглянемо деякі характеристики цього поняття.
Рівність вертикальних кутів
Рівність вертикальних кутів є їхньою основною властивістю. Що таке вертикальні кути по суті, так це кутові величини, які завжди рівні між собою. Наприклад, якщо один з кутів складає 45 градусів, то і його вертикальний партнер також буде 45 градусів.
Аплікативність в реальному світі
Вертикальні кути мають важливе значення не лише в теоретичній частині геометрії. Вони мають широке застосування в таких галузях, як:
- Архітектура: Дизайн і планування споруд часто враховують вертикальні кути для оптимізації простору і балансу структури.
- Інженерія: В основі розрахунків в механіці, зокрема, при вивченні сил і їхніх напрямків.
- Комп’ютерна графіка: Векторний аналіз і моделювання сцен часто використовують ці знання.
Властивості вертикальних кутів
Розглянемо кілька дуже важливих властивостей вертикальних кутів, які відіграють важливу роль в математичних розрахунках і чудово ілюструють їх значення у прикладних задачах.
Спільні властивості
- Вертикальні кути утворюються при перетині двох прямих, завжди дорівнюють один одному.
- Якщо одна пара вертикальних кутів дорівнює, то і інша пара автоматично також буде рівною.
- Вертикальні кути завжди мають центр симетрії у точці перетину прямих.
Практичне застосування знань про вертикальні кути
Розглянемо, як знання про вертикальні кути може бути корисне на практиці, як у професійних сферах, так і в повсякденному житті.
Приклади застосування
- Архітектурне проектування: Вертикальні кути використовуються для точного розрахунку несучих конструкцій і розташування елементів будівлі під кутом.
- Інженерна механіка: При аналізі силових структур відносно різних напрямків, вертикальні кути можуть допомогти в побудові правильних проекцій і розрахунків.
- Освіта: У навчанні геометрії для школярів і студентів вузів, знання та аналіз вертикальних кутів сприяє розвитку просторового мислення і логіки.
Приклади задач на вертикальні кути
Для кращого засвоєння матеріалу розглянемо кілька прикладів задач на вертикальні кути з їх розв’язанням:
Задача 1
Дві прямі перетинаються в точці O, і утворюють кути. Якщо один з вертикальних кутів дорівнює 60 градусів, то визначте величину всіх інших кутів.
Розв’язання:
- Якщо один з кутів дорівнює 60 градусів, то його вертикальний кут також дорівнює 60 градусів.
- Сусідній до нього кут буде мати величину 180 – 60 = 120 градусів (оскільки сусідні кути доповнюють один одного до 180 градусів).
- Відповідно, інший вертикальний кут також буде 120 градусів.
Задача 2
Дві прямі перетинаються і утворюють кути, серед яких один кут дорівнює (2x + 30^circ), а інший, його вертикальний кут дорівнює (4x – 10^circ). Знайти значення x та визначити величину всіх кутів.
Розв’язання:
- Оскільки кути вертикальні, вони рівні, тому можемо записати рівняння: (2x + 30 = 4x – 10).
- Розв’яжемо рівняння:
- Отримаємо: (2x + 30 = 4x – 10)
- (10 + 30 = 4x – 2x)
- (40 = 2x)
- (x = 20)
- Підставляючи х в первинні вирази для кутів, отримаємо:
- Перший кут: (2x + 30 = 2(20) + 30 = 70^circ)
- Другий кут: (4x – 10 = 4(20) – 10 = 70^circ)
- Таким чином, величини всіх кутів складають 70 градусів (вертикальні) та 110 градусів (доповнюють до 180).
Підсумок
Поняття, що таке вертикальні кути, відкриває безліч можливостей для розуміння геометричних структур і їхніх властивостей. Це не лише фундаментальна концепція, але й база для практичних застосувань у багатьох галузях. Розуміння і вміння працювати з вертикальними кутами розвиває математичне мислення, формує навички логічних викладок і є важливим елементом у загальній системі знань учня як початкової, так і старшої школи.
| Тип кута | Властивості |
|---|---|
| Вертикальні кути
|